Fractions: 2/3 Vs. 4/6 Explained With Visuals
Is it always true that two-thirds is the same as four-sixths? While it might seem like it at first glance, a closer examination reveals that this is a nuanced relationship, and the concept of equivalent fractions holds the key to understanding why.
The initial assumption might be that if we have a fraction, like 2/3, and we perform some operation on both the numerator and the denominator, we automatically get an equivalent fraction. Josh might believe that 2/3 is always identical to 4/6. However, as Meghan correctly points out, while 2/3 and 4/6 are equivalent fractions, meaning they represent the same overall value, they can indeed be different amounts depending on the context.
To truly grasp this, let's delve into the practical application. Imagine Diana and Becky, each taking part in a race. Diana runs a quarter mile straight down the street. Becky, on the other hand, runs a quarter mile on a track. Both cover the same distance a quarter of a mile. This is analogous to equivalent fractions: different representations, same value. We can visually represent this using fraction bars or geometric shapes. Consider fraction bars; they provide a clear visual demonstration that 2/3 is not always the same as 4/6 in a way that can be easily grasped.
Let's visualize the fractions using a different approach. Suppose we want to find out whether 2/3 is greater than 4/6. A quick glance might not provide the answer. However, understanding equivalent fractions makes it simpler to compare. Users can easily input these fractions into a calculator, which accepts fractions in the form of numerators and denominators, for example, '2/3' and '4/6'.
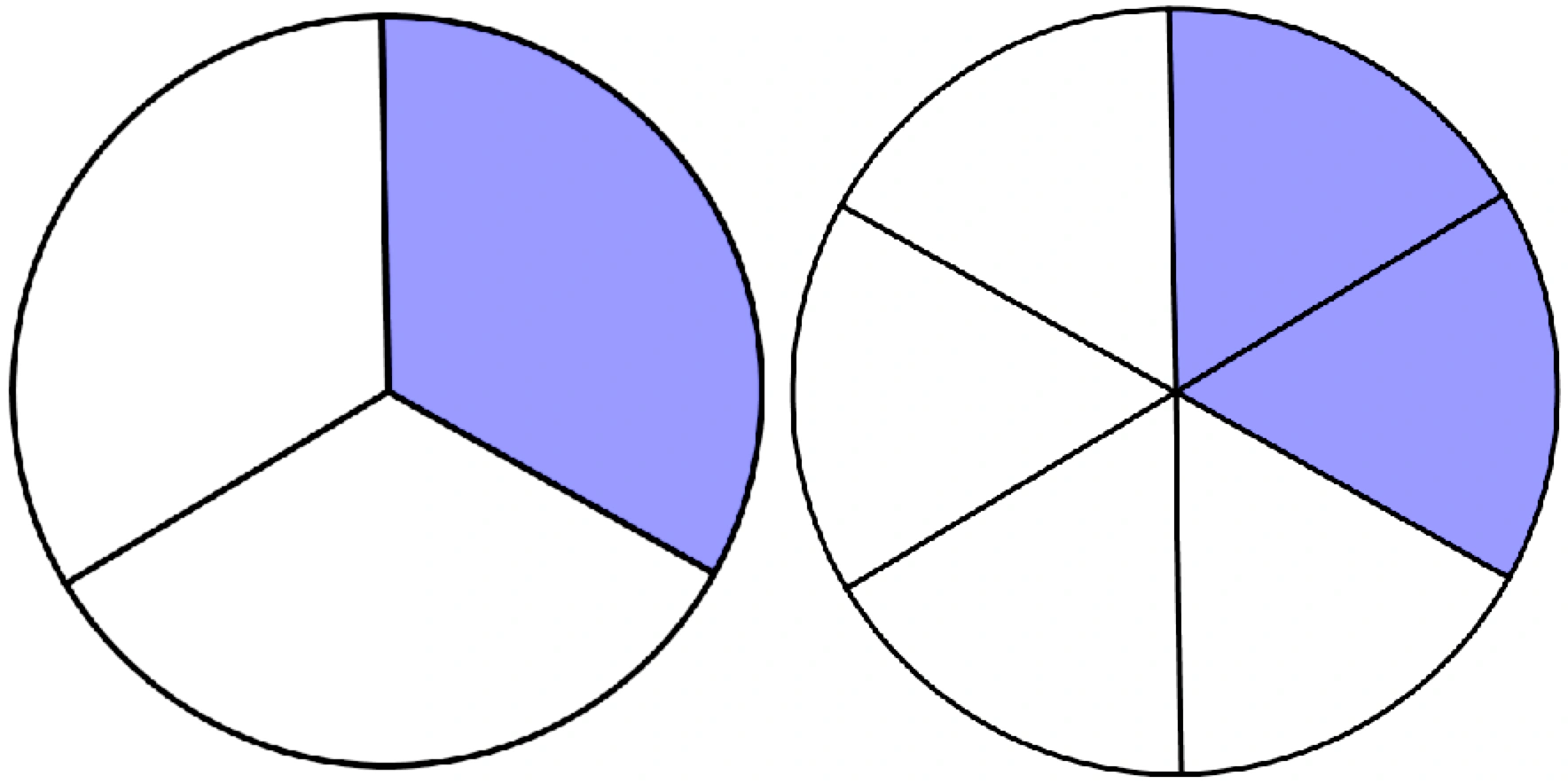
Now, let's consider another representation of a fraction. If we begin with a whole and divide it into thirds, we are dealing with the denominator (3). If we take two of those thirds (the numerator is 2), we have the fraction 2/3. Now, let's divide each of those thirds into two equal parts. The original whole is now divided into six parts. The two parts we had previously (the 2/3) now become four parts out of the six new parts, leading to the fraction 4/6. So, 4/6 is simply another representation of 2/3.
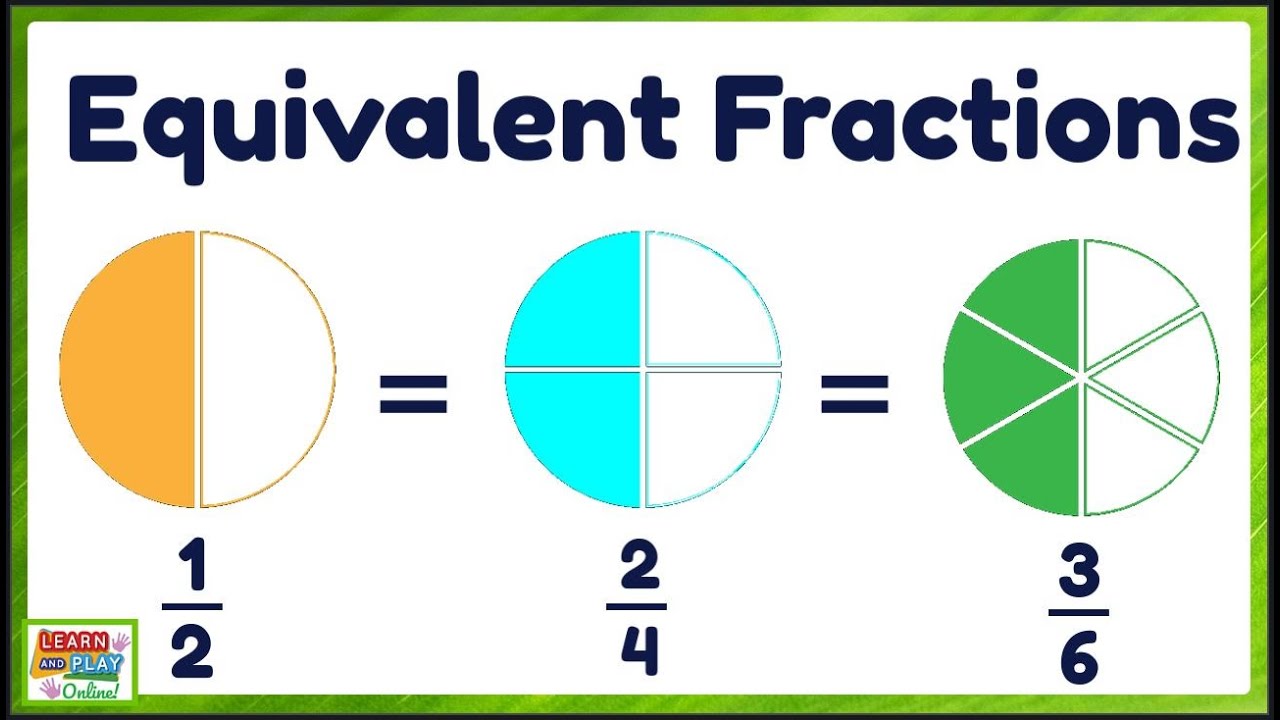
Equivalent fractions have the same value, but they can have different numerators and denominators. They are different ways of expressing the same proportion. The key principle here is that the numerator and the denominator must be divisible by the same number to generate an equivalent fraction. For example, let's consider the fraction 6/12. Both 6 and 12 are divisible by 2, resulting in the equivalent fraction 3/6. Furthermore, dividing both 6 and 12 by 3 yields 2/4. Alternatively, dividing both by 6 gives us 1/2.
To further understand, how can we find if two fractions are equivalent. There are several methods. One involves finding a common denominator, the least common denominator (LCD), for both fractions. Consider 2/3 and 4/6. The least common denominator of 3 and 6 is 6. The next step is to convert both fractions to equivalent fractions with a denominator of 6. For 2/3, since 3 multiplied by 2 equals 6, we multiply both the numerator and denominator by 2: (2 x 2) / (3 x 2) = 4/6. Indeed, 2/3 is equivalent to 4/6. Learn how to calculate if 2/3 is greater than 4/6 by converting it to a common denominator.
A different technique is cross-multiplication. Multiply the numerator of the first fraction by the denominator of the second. Then multiply the denominator of the first fraction by the numerator of the second. If the results are the same, the fractions are equivalent.
We can see the difference of fractions by taking the clock as the model for modular arithmetic. Weird still, even though youd think that 13 + 4 = 17, in this modulo 12 system, 14 + 4 = 6 because 6 pm represents 18 oclock.
In algebra, you will need to be able to work with numbers, words, and geometric representations.
Now consider this: to find three equivalent fractions for 4/6, we can multiply 4/6 by different forms of 1/1. For example, (4/6) (2/2) = 8/12. Another could be (4/6) (3/3) = 12/18. Or (4/6) * (4/4) = 16/24. The list is infinite. Note that we could also simplify 4/6 to 2/3 by dividing both numerator and denominator by 2.
Remember, the core concept here is the equivalence of fractions. Equivalent fractions have the same value, but can have different numerators and denominators.
Let's summarise, while 2/3 and 4/6 represent the same proportional value, they are not always the same "amount" in a concrete scenario. Diana and Becky running a quarter mile is the perfect example to highlight how fractional parts can be represented differently. The key is to consider the context.